
Proporção áurea
Introdução
- Proporção áurea, número de ouro, número áureo, secção áurea ou proporção de ouro é uma constante real algébrica irracional.
- Ela é representada pela letra grega Φ (PHI), em homenagem ao escultor Phideas (Fídias), podendo também que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. O número de ouro é ainda frequentemente chamado razão de Phidias.
- Também é chamada de seção áurea (do latim sectio aurea), razão áurea, razão de ouro, média e extrema razão (Euclides), divina proporção, divina seção (do latim sectio divina), proporção em extrema razão, divisão de extrema razão ou áurea excelência.
- Desde a Antiguidade, a proporção áurea é usada na arte. Este número está envolvido com a natureza do crescimento.
Matemática
- Dois valores positivos estão em razão áurea se sua razão é igual à razão da sua soma pela maior das quantidades. Algebricamente, dados a e b, onde a > b > 0, então:
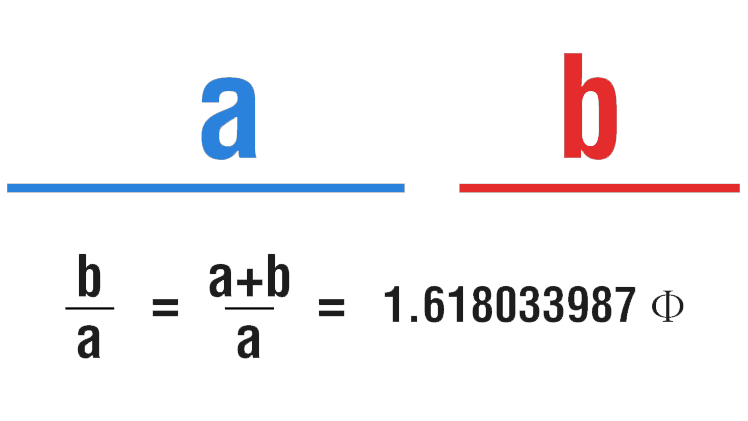
“Um segmento de reta se diz dividido em média e extrema razão, se a razão entre o menor e o maior dos segmentos é igual à razão entre o maior e o segmento todo.”
Definição da divisão em média e extrema razão de Euclides (Livro VI de Os Elementos).
Sequência de Fibonacci
- A razão áurea está presente na fórmula do termo geral da Sequência de Fibonacci, Sucessão de Fibonacci ou Série de Fibonacci que é uma sequência de números inteiros, começando normalmente por 0 e 1, na qual cada termo subsequente corresponde à soma dos dois anteriores.
- A sequência recebeu o nome do matemático italiano Leonardo de Pisa ou Leonardo Fibonacci, mais conhecido por apenas Fibonacci, que descreveu na obra Liber Abaci ou Livro do Ábaco (1202) o crescimento de uma população de coelhos, a partir desta. Esse livro foi resultado de estudos de Fibonacci com matemáticos sírios, gregos e egípcios. Esta sequência já era, no entanto, conhecida na antiguidade por gregos e indianos.
- Liber Abaci foi um dos primeiros livros ocidentais a descrever os algarismos arábicos, introduzindo na Europa a numeração árabe (em substituição a numeração romana) e esclarecendo o funcionamento desta numeração e do zero.
- A ideia era responder: Quantos pares de coelhos existirão daqui a um ano?
Fₙ=Fₙ₋₁+Fₙ₋₂, onde a sequência inicial F₁ = 1 e F₂ = 1.
Fórmula da Sequência de Fibonacci
- Fibonacci considerou o crescimento de uma população idealizada (não realista biologicamente) de coelhos. Os números descrevem o número de casais na população de coelhos depois de n meses se for suposto que:
- No primeiro mês nasce apenas um casal;
- Casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida;
- Não há problemas genéticos no cruzamento consanguíneo;
- Todos os meses, cada casal fértil dá a luz a um novo casal; e
- Os coelhos nunca morrem.

- Os números de Fibonacci são, portanto, os números que compõem a seguinte sequência:0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … .
- É importante destacar que a sequência de Fibonacci é infinita. Portanto, o ideal é que você defina um valor que tenha como objetivo e, ao alcançar esse objetivo, você decida uma nova meta para alcançar.
- Mas genericamente, chama-se sequência de Fibonacci qualquer função g tal que g(n + 2) = g(n) + g(n + 1). Essas funções são precisamente as de formato g(n) = aF(n) + bF(n + 1) para alguns números a e b, então as sequências de Fibonacci formam um espaço vetorial com as funções F(n) e F(n + 1) como base.
- Em particular, a sequência de Fibonacci com F(1) = 1 e F(2) = 3 é conhecida como a sequência de Lucas. A importância dos números de Lucas L(n) reside no fato deles gerarem a Proporção áurea para as n-ésimas potências.
![{\displaystyle F(n)={\frac {\phi _{+}^{n}-\phi _{-}^{n}}{\phi _{+}-\phi _{-}}}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3800d742e7a9b1d96a05bbd71eb197028208b3be)
- O número áureo pode ser aproximado pela divisão do n-ésimo termo da Série de Fibonacci pelo termo anterior, sendo a aproximação tanto melhor quanto maior for n. Por exemplo:
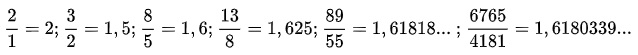
Triângulo de Pitágoras
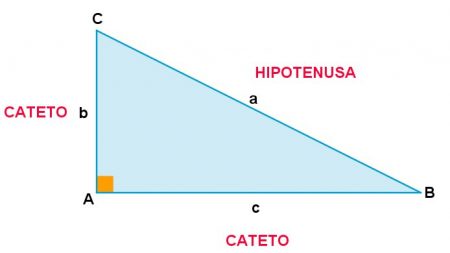
- O triângulo de Pitágoras é um triângulo retângulo, ou seja, um dos seus ângulos é reto, mede 90°. A hipotenusa é o lado oposto ao ângulo reto e os lados próximos ao ângulo reto são os catetos. No triângulo retângulo o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos, que é o teorema de Pitágoras (a² = b² + c²).
- Apesar de ser creditada a demonstração disso para Pitágoras, existem suspeitas que os matemáticos babilônicos já tinham métodos para realizar essas medidas.
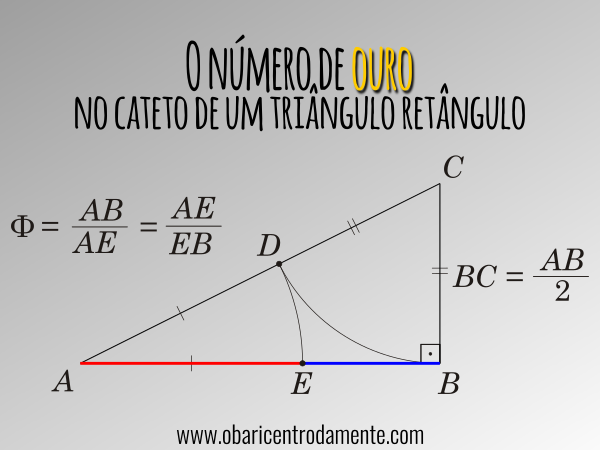
- Em um triângulo retângulo onde um dos catetos é a metade do outro, existe um ponto no cateto maior que o divide em média e extrema razão e pode ser construído com régua e compasso. Se o cateto BC é metade do cateto AB. Então o ponto E divide o cateto AB em média e extrema razão e pode ser obtido descrevendo apenas dois arcos de circunferência.
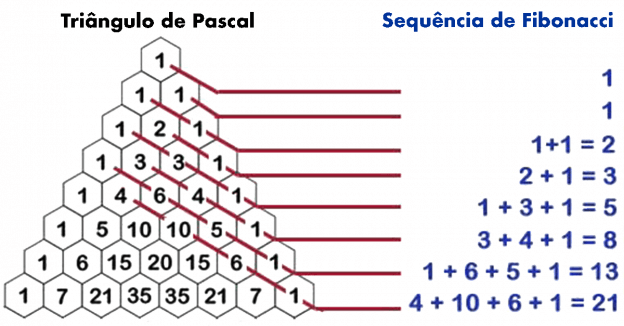
Triângulo de Pascal
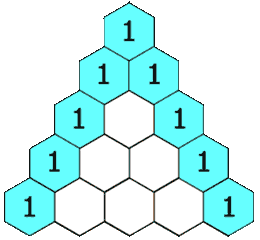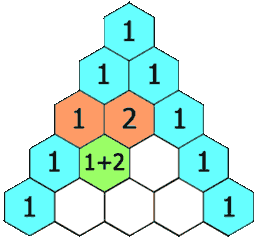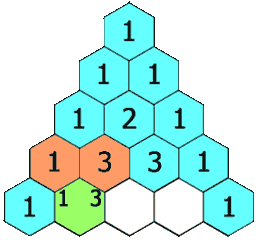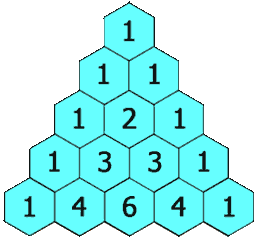
- O triângulo de Pascal ou triângulo de Tartaglia é um triângulo numérico infinito formado por números binomiais, onde cada número do triângulo de Pascal é igual à soma do número imediatamente acima e do antecessor do número de cima.
- O triângulo de Pascal e o triângulo de Pitágoras também se relacionam com a sequência de Fibonacci que, por sua vez, tem relação com a razão áurea.
Triângulo áureo
- Um triângulo de ouro, triângulo áureo ou triângulo sublime é um triângulo isósceles, ou seja, possui dois lados com a mesma medida, no qual a divisão do comprimento de um dos lados iguais pelo da base é o número de ouro:
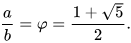
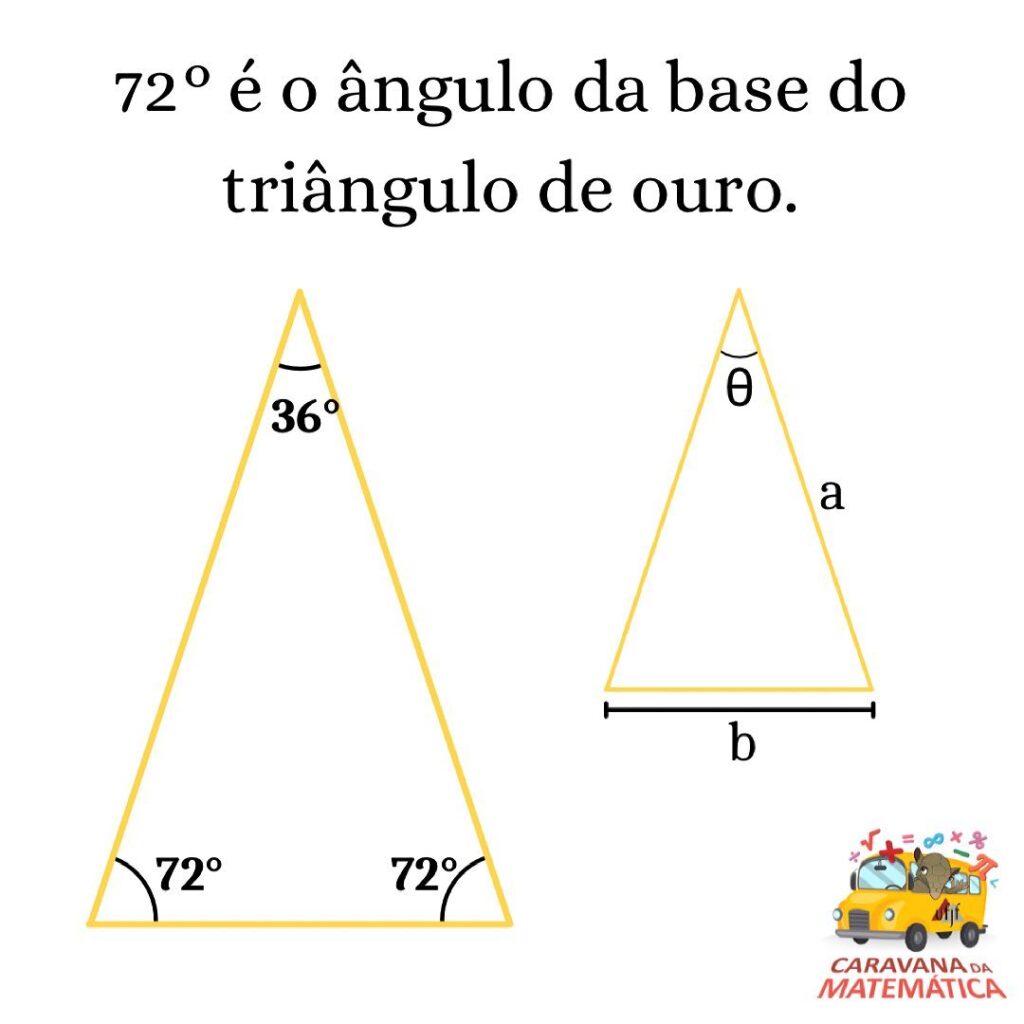
- A divisão do do lado maior, pelo menor, resulta no número áureo. Assim, traçando-se uma bissetriz (semirreta que divide ao meio em dois ângulos congruentes) em um de seus dois ângulos de 72°, surge um novo triângulo, semelhante ao maior, e repetindo a operação, isso acontece infinitas vezes, assim como o retângulo áureo.
Retângulo áureo
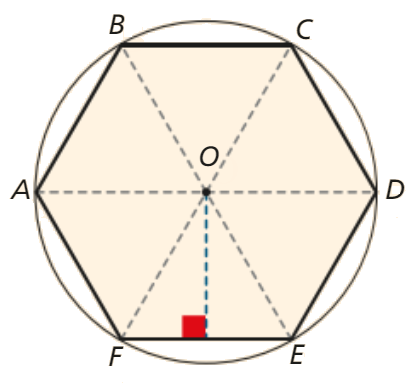
- O retângulo de ouro é formado pela divisão em média e extrema razão de Euclides. Ele é assim chamado porque ao dividir-se a base desse retângulo pela sua altura, obtêm-se o número de ouro.
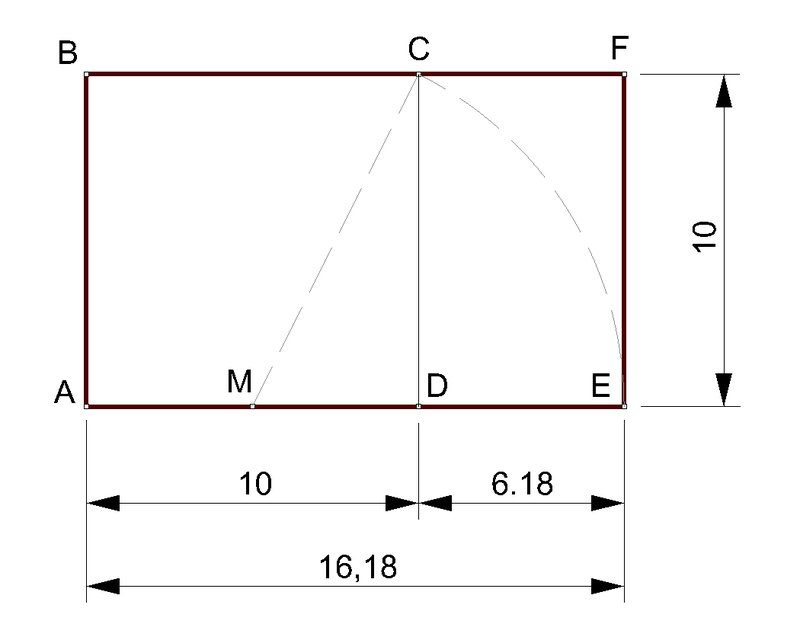
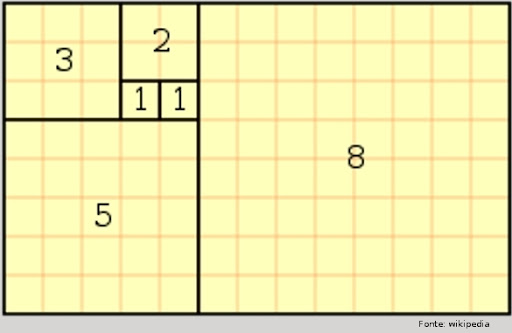
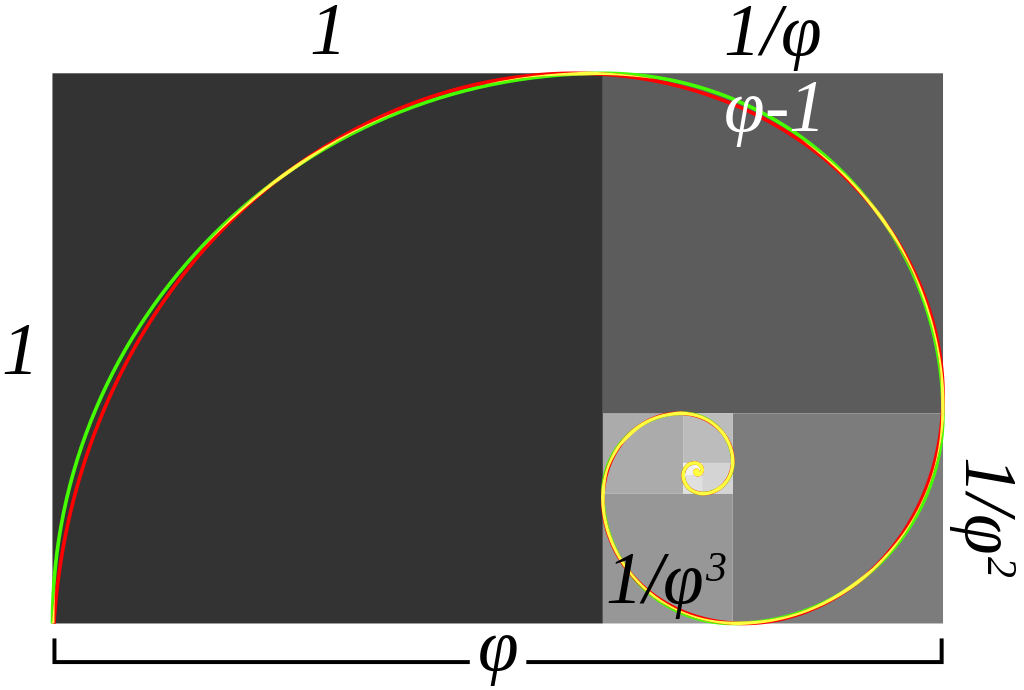
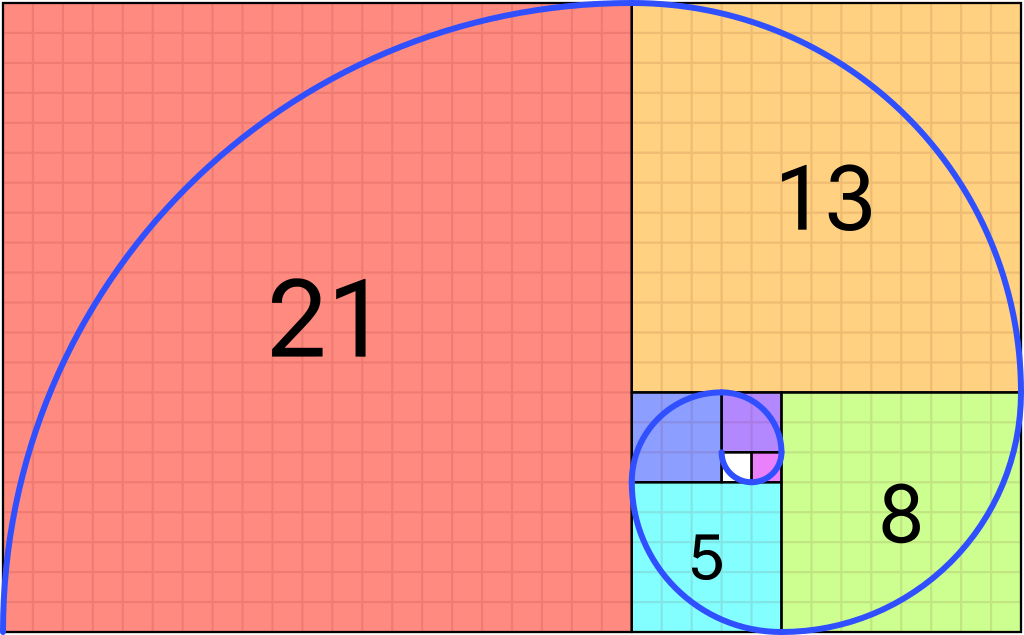
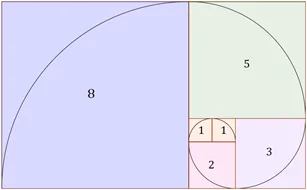
Espiral áurea
- A espiral áurea é uma espiral logarítima cujo fator de crescimento é a proporção áurea. A espiral áurea fica mais larga por um fator de proporção áurea para cada quarto de volta que dá.
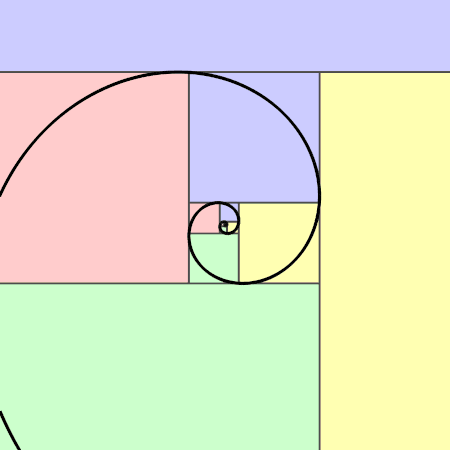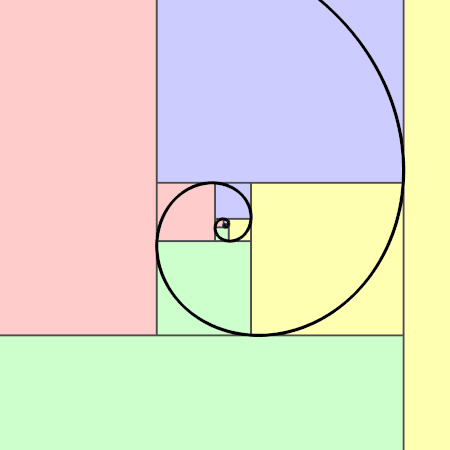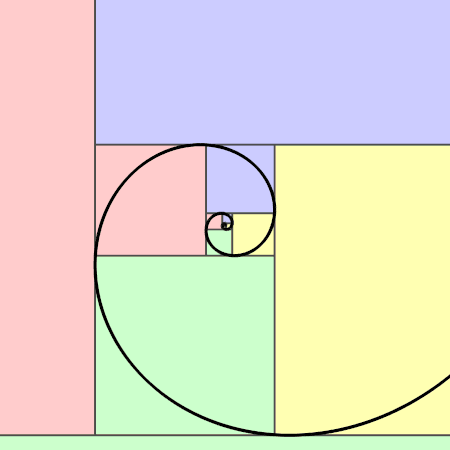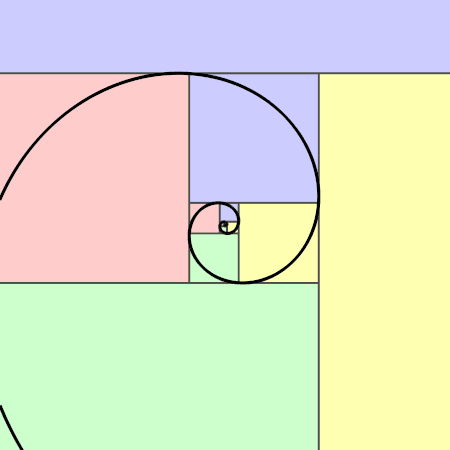
Pitagóricos
- Os primeiros filósofos gregos, chamados de pré-socráticos tinham como preocupação a cosmologia, ou seja, como o universo era formado, buscando por argumentos lógicos e não mitológicos. Perguntas comuns entre os pré-socráticos são: Como surgiu o universo a partir do caos? Qual era o elemento que formava todas as coisas?
- Devido ao assunto que trazemos hoje, eu apresento Pitágoras de Samos (em grego: Πυθαγόρας ὁ Σάμιος, ou apenas Πυθαγόρας; Πυθαγόρης em grego jônico; Samos, cerca 570 – Metaponto, cerca 495 AEC) que foi um filósofo pré-socrático e matemático grego jônico creditado como fundador do movimento chamado Pitagorismo, onde seus adeptos eram os pitagóricos. Para eles, o universo tinha como elemento fundamental os números.
- Na sua maioria, as informações sobre Pitágoras foram escritas séculos depois da sua morte, de modo que há pouca informação confiável sobre ele. Nasceu na ilha de Samos e viajou pelo Egito e pela Grécia. Em 520 AEC voltou a Samos. Cerca de 530 AEC, mudou-se para Crotona, na Magna Grécia.

- Os pitagóricos interessavam-se pelo estudo das propriedades dos números – para eles o número (sinônimo de harmonia) era considerado como essência das coisas – é constituído então da soma de pares e ímpares, noções opostas (limitado e ilimitado) respectivamente números pares e ímpares expressando as relações que se encontram em permanente processo de mutação. Teriam chegado à concepção de que todas as coisas são números.
- Os pitagóricos se dispersam e passam a atuar amplamente no mundo helênico, levando a todos os setores da cultura o ideal de salvação do homem e da pólis através da proporção e da medida.
- Representação geométrica dos elementos:
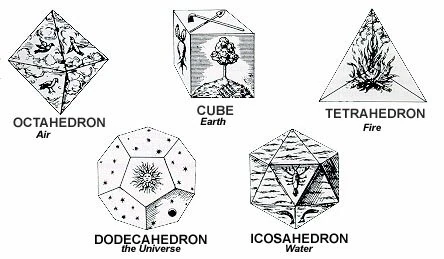
“… o princípio das matemáticas é o princípio de todas as coisas…”
Pitágoras de Samos.
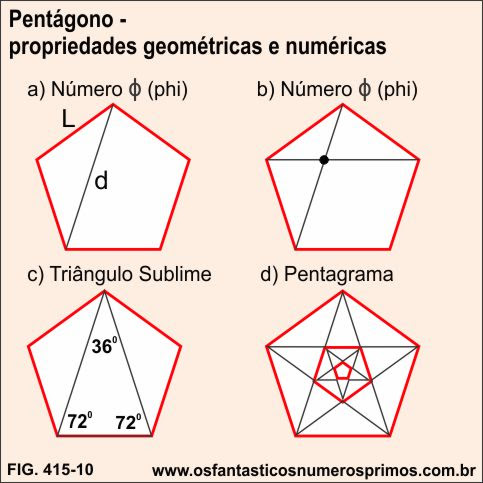
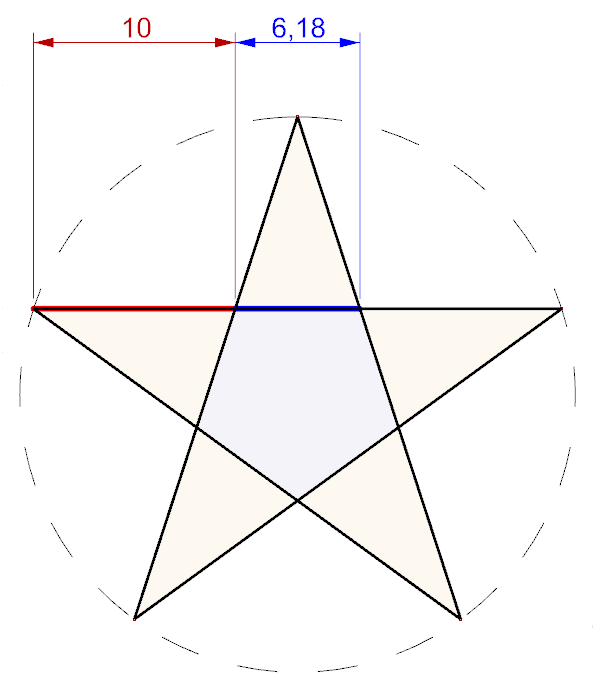
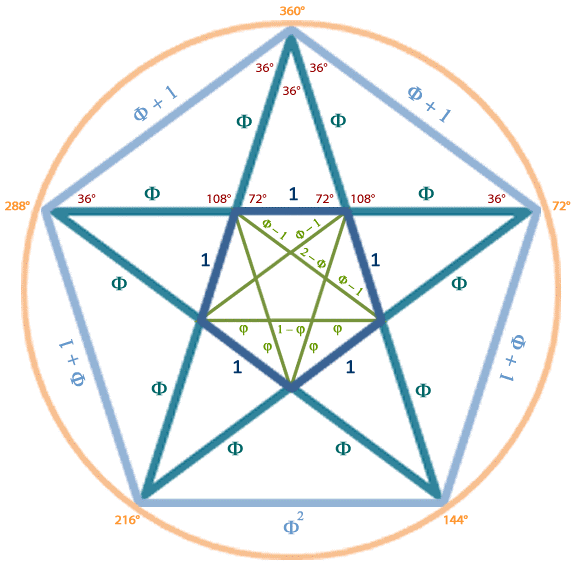
- O pentagrama, ou pentágono estrelado tornou-se símbolo da Escola Pitagórica, e era uma figura envolvida em misticismo. Em um pentágono regular as diagonais se cruzam, formando um novo pentágono interno. A interseção de duas diagonais divide-as de uma forma especial, chamada razão áurea. Este valor é chamado de “número de Ouro”.

Natureza
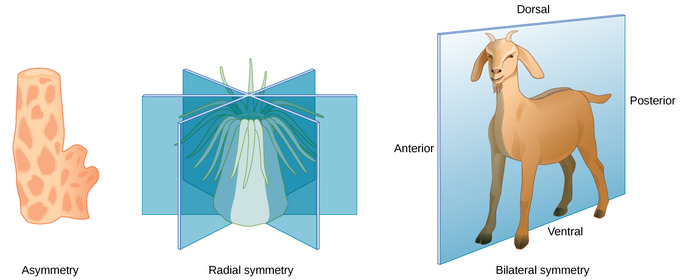
- Na natureza, o padrão de crescimento dos seres vivos seguem simetrias ou são assimétricos (esponjas). Quando falamos dos simétricos, que são aqueles que podem ser divididos em partes semelhantes, eles podem possuir:
- Simetria esférica – Onde qualquer plano que passe pelo centro da esfera gera partes iguais. Não é presente em animais, mas é presente em seres vivos como plantas e fungos;
- Simetria radial – Onde os planos que passam pelo centro formam partes iguais apenas em sentido longitudinal, tendo uma porção anterior e posterior diferentes se cortar em um plano transversal. Exemplo: Equinodermos como a estrela-do-mar, e cnidários como a anênoma;
- Simetria bilateral – Onde existe um único plano possível para separar em partes iguais. Exemplo: mamíferos como humanos e cachorros.
- Alerta! É importante ressaltar que esse tipo de argumento de simetria acaba sendo confundido com a lei áurea e usado em discursos que defendem a existência de corpos com padrões de beleza. Ninguém, absolutamente ninguém, humano ou não, é perfeitamente simétrico. Inclusive, existem seres como os equinodermos que nascem com simetria bilateral e só depois de adultos possuem simetria radia. Não se cobre para ser simétrico. O nosso conjunto genético e o ambiente geram pressões para que sejamos diferentes até nos nossos eixos de simetria. Essa discussão é apenas teórica e imaginativa e não se reflete na realidade dos seres.
- Apesar da diversidade da natureza tornar todas as criaturas especiais de uma forma ou de outra, é possível, de maneira teórica, ver padrões próximos ao encontrado na lei áurea em diversas estruturas com origem em seres vivos.
- Pode ser encontrado de forma aproximada no homem (o tamanho das falanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
- Justamente por ser encontrado em estudos de crescimento, o número de ouro ganhou um status de “ideal”, sendo alvo de pesquisadores, artistas e escritores. O fato de ser apoiado pela matemática é que o torna fascinante, mas também perigoso podendo reforçar padrões de beleza longe dos reais.

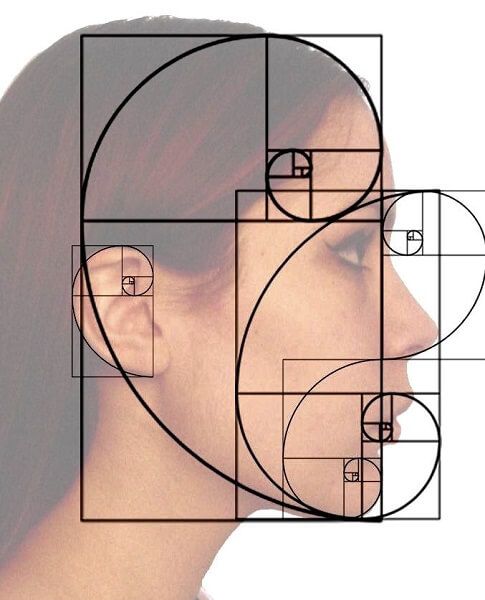
- A sequência de Fibonacci corresponde às medidas dos lados dos quadrados que lembram a espiral logarítmica muito encontrada em formas da natureza como a do molusco náutico (Nautilus pompilius). No entanto, existe uma variedade de ângulos de crescimento de conchas de moluscos que podem ser diferentes da espiral áurea, apesar de lembrar elas.
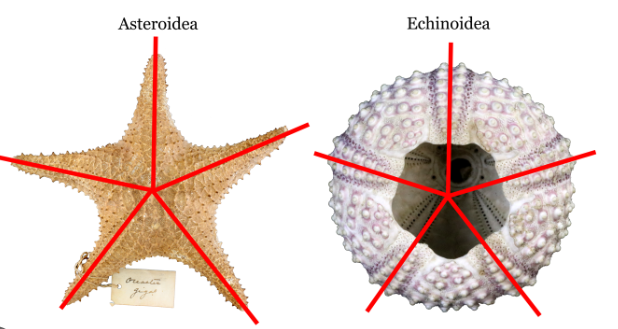
- Muitos animais e plantas possuem seus corpos com eixos de simetria em pentagrama, reproduzindo a lei áurea muitas vezes como equinodermos adultos (ouriços-do-mar, crinóides, estrelas-do-mar e bolachas-do-mar) e flores de muitas plantas.



Artes
- Na literatura, o número de ouro encontra sua aplicação mais notável no poema épico grego Ilíada, de Homero, que narra os acontecimentos dos últimos dias da Guerra de Troia. Quem o ler notará que a proporção entre as estrofes maiores e as menores dá um número próximo a 1,618, o número de ouro.
- Obras da arquitetura clássica, como o Parthenon, templo dedicado a deusa Atena presente na Acrópole da cidade de Atenas, na Grécia, revelam o uso da razão áurea na busca de uma harmonia estética.


- A Mona Lisa, de Leonardo da Vinci, tem a proporção áurea nas relações entre o tronco e a cabeça, bem como nos elementos da face. Medições feitas por computador mostraram que os olhos de Mona Lisa estão situados em subdivisões áureas da tela.

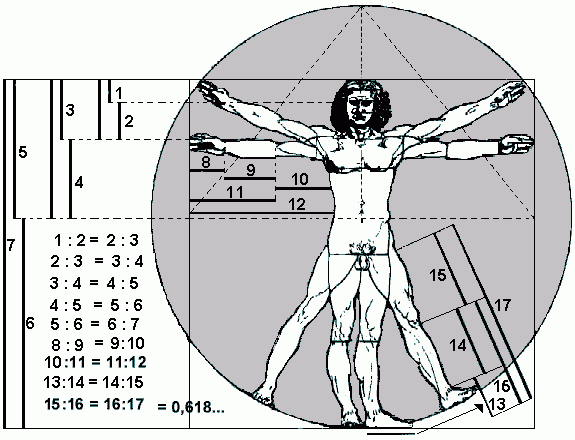
- Leonardo Da Vinci acreditava na perfeição da figura humana e considerava as medidas e o funcionamento do corpo humano como uma analogia das medidas e funcionamento do universo, todas conectadas pela proporção do número de ouro.
- O número de ouro também está presente em diversas obras de compositores clássicos, sendo o exemplo mais notável a famosa sinfonia n.º 5, de Ludwig van Beethoven.
- É possível ver o retângulo de ouro em prédios como a catedral de Notre Dame e a sede da Organização das Nações Unidas (ONU).




Bruxaria
- Para mim, a proporção áurea é um dos grandes mistérios divinos que os matemáticos tiveram um vislumbre. Sem falar que mostra que ciência e religião quando conseguem atuar de forma complementar conseguem explicações muito mais belas e completas sobre o nosso mundo.
- Ter conhecimento dessas formas geométricas sagradas te gera mais uma camada de conhecimento no seu arsenal simbólico para perceber o toque das divindades no seu dia a dia. Sem falar que pode ajudar muito ritualisticamente, solte a sua criatividade. Aqui darei alguns exemplos.
- Saber que o pentagrama também tem essa camada de significado o torna ainda mais poderoso. Inclusive podendo ser por si só um altar poderoso. Ou buscar por flores que tenham esse formato de cinco pétalas para ser o centro do seu altar.
- Você pode usar esses formatos mágicos para trabalhar com cristais, plantas ou animais que tenham uma conformação geométrica interna específica de acordo com a sua intenção.
- Você pode construir templos, distribuir móveis, criar sigilos, mandalas ou distribuir os itens de um ritual sobre o seu altar utilizando esses formatos.
- Inclusive você pode usar desses símbolos e formatos geométricos para consagrar instrumentos mágicos.



Referências
- Saboya, M. C. L. (2015). Pitágoras: todas as coisas são números. Educação, Gestão e Sociedade: revista da Faculdade Eça de Queirós, ISSN 2179-9636, 5 (19).
- Proporção áurea. Disponível em <https://pt.wikipedia.org/wiki/Propor%C3%A7%C3%A3o_%C3%A1urea> Acessado em 17/04/2024.
- Sequência de Fibonacci. Disponível em <https://pt.wikipedia.org/wiki/N%C3%BAmero_de_Fibonacci> Acessado em 17/04/2024.
- Sequência de Fibonacci, razão áurea e o Número de Ouro. Disponível em <https://islogic.medium.com/sequ%C3%AAncia-de-fibonacci-raz%C3%A3o-%C3%A1urea-e-o-n%C3%BAmero-de-ouro-7f300a1a5a64> Acessado em 17/04/2024.
- Triângulo de ouro. Disponível em <https://pt.wikipedia.org/wiki/Tri%C3%A2ngulo_de_ouro#:~:text=Um%20tri%C3%A2ngulo%20de%20ouro%20%C3%A9,72%C2%B0%20e%2072%C2%B0.> Acessado em 17/04/2024.
- Triângulo de Pascal. Disponível em <https://pt.wikipedia.org/wiki/Tri%C3%A2ngulo_de_Pascal> Acessado em 17/04/2024.
- O número de ouro no cateto de um triângulo retângulo. Disponível em <https://www.obaricentrodamente.com/2018/08/o-numero-de-ouro-no-cateto-de-um-triangulo-retangulo.html> Acessado em 17/04/2024.
- Retângulo de ouro. Disponível em <https://pt.wikipedia.org/wiki/Ret%C3%A2ngulo_de_ouro> Acessado em 17/04/2024.
- Espiral áurea. Disponível em <https://en.wikipedia.org/wiki/Golden_spiral> Acessado em 17/04/2024.





